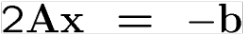Robotlar için Lineer Cebir

tarihinde gönderilmiş tarafından

VECTORS (VEKTÖRLER)

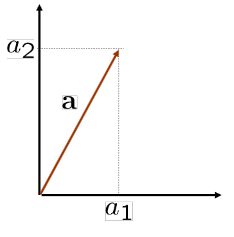
  • Yönü ve büyüklüğü olan doğru parçası

  • Sayılar dizisi

  • n boyutlu uzaylarda bir noktayı temsil ederler.

2.png
x=[1 2 3 4];
y=[5 6 7 8];

 

 

 

Scalar Product (Skaler Çarpım)

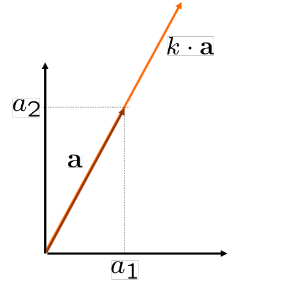
  • Skaler-vektör çarpım; “k.a”

  • Vektörün sadece uzunluğunu değiştirir,yönünü değil

3.png
>> x=[1 2 3 4];
>> k=2;
>> k*x
2468

Sum (Toplam)

  • Vektörlerde toplama işlemi;

4.png

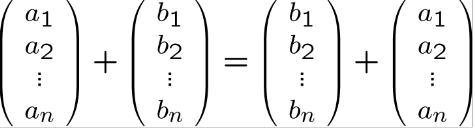
  • Bunu zincirleme veya ucuca ekleme olarak görselleştirebiliriz.

5.png
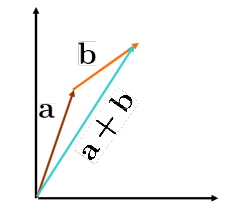
>> x=[4 5 2];
>> y=[1 2 6];
>> x+y

ans =

     5     7     8

Dot Product (Nokta Çarpım)

  • Vektörlerde iç çarpım (inner product);

6.png
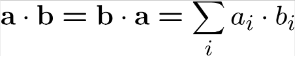
x=[4 5 2];
y=[1 2 6];
dot(x,y)

ans =

    26

  • V iç çarpım ve x, y ?V olsun. Eğer = 0 ise x ve y ye ortogonal (dik) vektörler denir.

  • İki vektör arasındaki açı, ifadesinde cos ? = 0 ise x , y ortogonal vektörler, cos ? = ± 1 yani = ± || x|| || y|| ise x ve y vektörleri paralel vektörlerdir.

>> y=[1 2 6];
>> norm(y)

ans =

    6.4031

Linear (In)Dependence (Lineer Bağımlılık)

  • b lineer doğrusal vektör olarak tanımlansın;

8.png

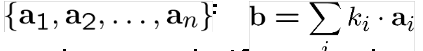
  • Başka bir deyişle, b vektörü ailerin k skaleriyle çarpımlarının toplamları şeklinde ifade edilebilir.

  • Eğer ki ler yoksa b , ai ye lineer bağımlı değildir.

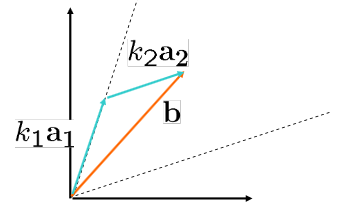
10.png

MATRICES (MATRİSLER)

  • Matrisler değer tablosu olarak yazılırlar, birçok kullanım şekilleri vardır.

11.png
>> A=[1 2 3;4 5 6;7 8 9]

A =

     1     2     3
     4     5     6
     7     8     9

Matrices as Collections of Vectors

Kolon Vektörleri (Column Vektors)

11.png

Satır Vektörleri (Row Vectors)

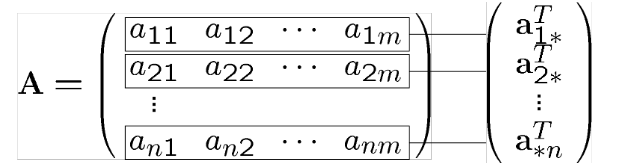
13.png

Matrices Operations ( Matris İşlemleri)

  • Sum (commutative, associative)

  • Product (not commutative)

  • Inversion (square, full rank)

  • Transposition

  • Multiplication by a scalar

  • Multiplication by a vector

Matrix Vector Product (Matris Vektör Çarpım)

  • Nokta çarpımında A.b nin bileşeni “i” olmak üzere ;

  • A.b vektörü bi katsayıları ile a*iye lineer bağımlıdır.

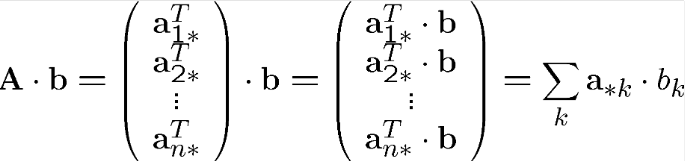
14.png

  • Eğer kolon vektörleri referans sistemi temsil ediyorsa, A.b çarpımı b vektörünün a*i ye göre küresel dönüşümünü hesaplar.

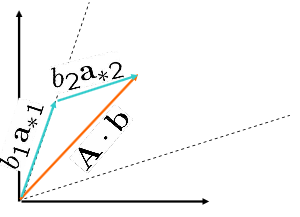
15.png

  • Her ai,j doğrusal bir karıştırma katsayısı olarak görülebilir, bu (A.b)j ye nasıl katkıda bulunduğunu gösterir.

  • Örneğin; çok boyutlu fonksiyonların Jakobiyenti

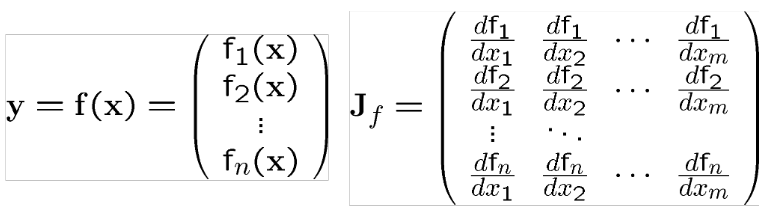
16.png

Matrix Matrix Product (Matris-Matris Çarpım)

Şu şekillerde tanımlanabilir;

  • Satır ve sütun vektörlerinin noktasal çarpımı

  • A ve B sütun vektörlerinin skalerleri ile lineer kombinasyonu

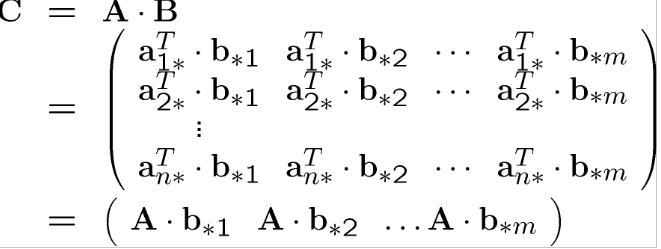
17.png

  • İkinci yorumu incelediğimizde C sütunlarının B sütunlarından A ya kadar izdüşümleri olduğunu görürüz.

  • Matrisler için yapılan tüm yorumlar vektör çarpımına dayanır.

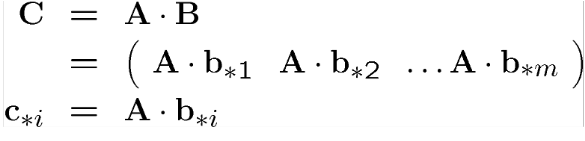
18.png
>> A=[2 4 3;2 1 1 ;4 6 5];
>> B=[2 1 5;-3 -2 1;0 4 -2];
>> A*B

ans =

    -8     6     8
     1     4     9
   -10    12    16

Linear Systems (Lineer Sistemler)

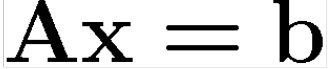
20.png

  • b Ax dönüşümünün bir sonucu iken x koordinatları A referans sisteminde bulunur.

  • Birçok çözüm yöntemi bulunur.

  • Sistem alttan veya üstten sınırlandırılmalıdır.

  • Bir (A’ b’) matrisini göz önüne alarak ve lineer olarak bağımlı tüm satırları bastırarak azaltılmış bir (A b) sistemini elde edebilirsiniz.

  • A’ nın lineer bağımsız sütunlarının veya satırlarının sayısı b’ nin boyutundan büyükse sistem üstten sınırlıdır.

  • Üstten sınırlı bir sistemde çözüm bulunamaz ancak pseudo inversion çözümü bulunabilir.

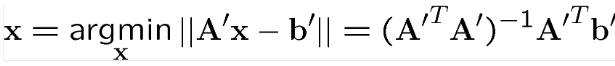
22.png

  • A’ nın lineer bağımsız sütünlarının veya satırlarının sayısı b’ nin boyutundan küçükse sistem alttan sınırlıdır.

  • Alttan sınırlı sistemler sınırsız çözüm kabul eder.Sonsuzluğun derecesi rank(A’)-dim(b’)

  • Bir matrisin rankı lineer bağımsız satır veya sütunların maksimumudur.

Matrix Inversion (Ters Matris)

23.png

  • A full ranklı bir kare matris ise yukarıdaki denklemin geçerli olduğu şekilde tek bir B=A-1 matrisi vardır.

  • A nın i. satırı ve A-1 nın j. sütunları;

i=j ise ortogonal

diğer durumlarda skaler çarpım 1 dir.

  • A-1 in i. sütunu aşağıdaki sistemin çözümü ile bulunabilir;

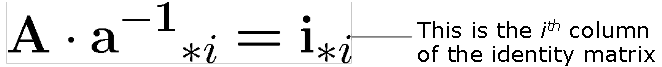
24.png
>> A=[2 3;5 1];
>> rank(A)

ans =

     2

>> B=inv(A)

B =

   -0.0769    0.2308
    0.3846   -0.1538

>> C=A*B

C =

    1.0000         0
   -0.0000    1.0000

Trace (İz)

  • Sadece kare matrislerde tanımlıdır.

  • Köşegen elemanlarının toplamı ;

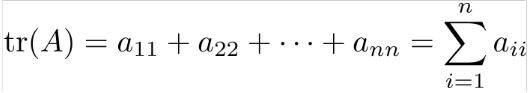
25.png

  • Aşağıdaki özelliklere sahip lineer bir operatördür;

Additivity:

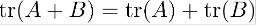
26.png

Homogeneity:

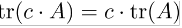
27.png

Pairwise commutative:

28.png

Trace is similarity invariant:

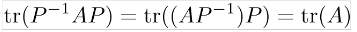
29.png

Trace is transpose invariant

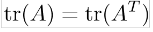
30.png
A=[2 -3 5;1 2 7;-1 0 1];
trace(A)
ans =

     5

Rank

  • Lineer bağımsız satır veya sütunların maksimum sayısı.

  • f(x)=Ax dönüşüm görüntüsünün boyutu

  • A, mxn matrisi iken;

-rank(A)>=0 ve eşitlik sağlanır ancak ve ancak A sıfır matristir.

-rank(A)> a=[2 4 4;2 3 1;3 2 5]; >> rank(a) ans = 3

Determinant

  • Sadece kare matrislerde tanımlıdır.

  • Hatırlayın, det(A)=0 olmadığı durumlar için AxA-1=I idi.

  • 2×2 lik matris için A=[aij ] için;

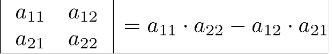
31.png

  • 3×3 lük matris için;

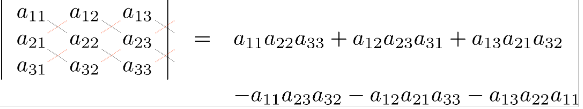
32.png

  • mxn genel matris için;

A matrisinin i. satır ve j. sütununa sahip Aij altmatrisini alalım.

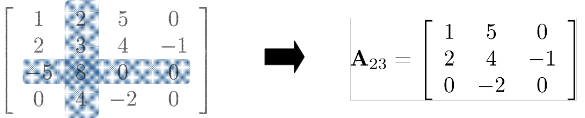
33.png

3×3 lük matris için determinantı yeniden yazalım;

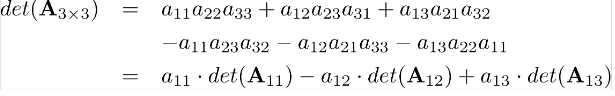
34.png

nxn lik matris için yazalım;

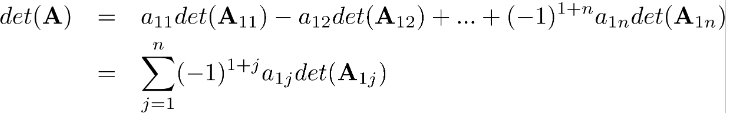
35.png

  • Cij=(-1)i+jdet(Aij) kofaktörünü (cofactor) alalım;

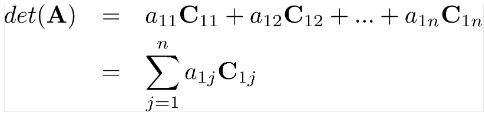
36.png

bu işleme ilk satır için kofaktör açılımı (cofactor expansion) denir.

>> A=[2 -3 5;1 2 7;-1 0 1];
>> det(A)

ans =

    38

problem: 25×25 lik bir matris alalım. Kofaktör açılımı n! tane çarpım gerektirir. n=25 için bu 1.5×1025 çarpımdır ve bunu modern bilgisayarlar 500.000 yılda alır .

  • Birçok hızlı metod vardır, Gauss elimination ile matrisi üçgensel hale indirgeyebiliriz.Buradan;

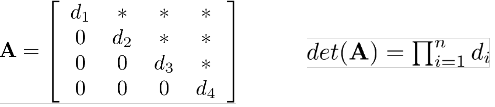
37.png

Çünkü üçgen matrisler için determinant, diyagonal elemanların çarpımıdır.

>>  a=[2 4 4;2 3 1;3 2 5];
>> diag(a)

ans =

     2
     3
     5

Determinant Özellikleri;

  • Satır İşlemleri: (A nxn kare matris)

-Eğer B, A matrisinin iki satırının değiştirilmesinden oluşuyorsa det(B)=-det(A) dır.

-Eğer B, A matrisinin bir satırının c sabit sayısıyla çarpımından oluşuyorsa det(B)=c.det(A) dır.

-Eğer B, A matrisinin bir satırının diğer satırıyla toplamından veya çarpımından oluşuyorsa det(B)=det(A) dır.

  • Transpoz: det(A)=det(AT)

  • Çarpım: det(A.B)=det(A).det(B)

Determinant Uygulamaları;

  • Ters matris bulma: (A-1) ters matris , adj(A) adjugate (ek) matis olmak üzere) A-1=adj(A)/det(A)

  • Özdeğerler: Karakteristik polinom bulma, det(A- ? .I)=0

  • Alan ve Hacim: alan=det(A)

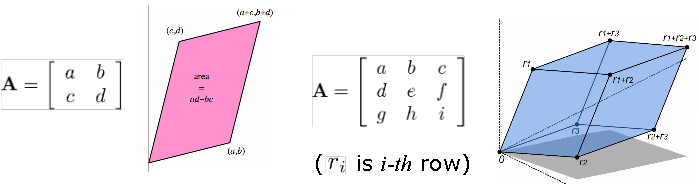
39.png
>> A=[1 2 3;2 4 -5;3 -5 6];
>> eig(A)

ans =

   -3.0773
    3.8414
   10.2359

Orthogonal Matrix (Ortogonal Matris)

  • Bir Q matrisi satır veya sütunlarının ortonormal bazı ile ifade edilebiliyorsa ortogonal matris dir.

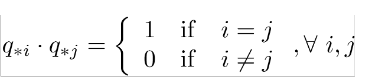
40.png

  • Lineer dönüşüm olarak, norm korunur ve öklid uzayında bir izometri (isometry) görevi görür.(yansıma-reflection ve dönüşüm-rotation)

  • Bazı özellikler;

Q.QT=QT.Q=I

1=det(I)=det(QQT)=det(Q).det(QT)=det(Q)2

Rotational Matrix (Dönüşüm Matrisi)

  • Robotikte önemli;

    • 2D rotasyon:

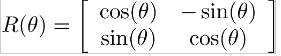
41.png

–3D rotasyon:

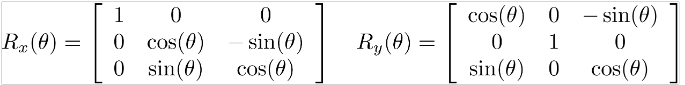
42.png
43.png
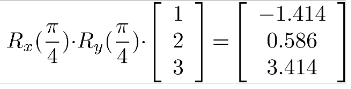
44.png
45.png
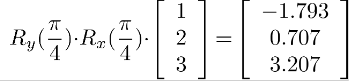
46.png

  • Rotasyon değişmeli değildir!

Matrices as Affine Transformations (Afin Dönüşümler Olarak Matrisler)

  • Bir 3D dönüşüm matrislerle kolay ve hızlı bir şekilde tanımlanabilir.

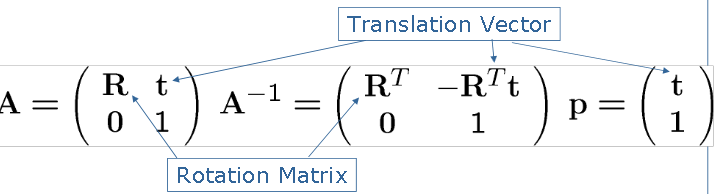
47.png

  • 2D ve 3D de homojen davranım

  • Dönüşümlerin değişimli olmadığını doğal olarak hesaba katar.

Combining Transformations (Dönüşümleri Birleştirme)

  • Basit bir yorum olarak; (homojen matrislerle ifade edilir) dönüşümlerin zincirlenmesi

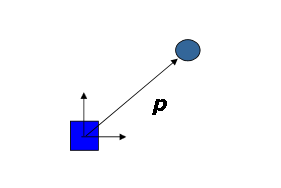
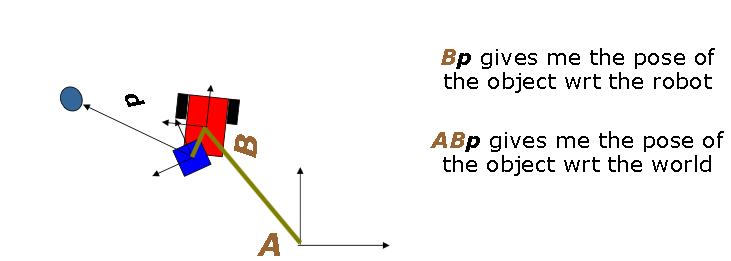
    • A matrisi robotun uzaydaki pozu,

    • B matrisi sensörün robot üzerindeki konumunu temsil etsin,

    • Sensör belirli bir p konumunda nesneyi kendi çerçevesinde algılar,(sensörün yeri hakkında ipucu yok)

    • Nesne küresel çerçevede nerededir?

50.png
48.png
49.png

Symmetric Matrix (Simetrik Matris)

  • A=AT ise A matrisi simetriktir.

  • A=-AT ise A matrisi simetrik değildir.

  • Her simetrik matris;

    • D=QAQT kosegenlestirilebilir, burada D ozdegelerin bir kosegen matrisidir ve Q, sutunlari A’nin ozvektorleri olan bir ortogonal matristir

    • Karesel formda tanımı;

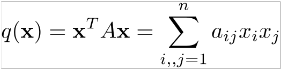
51.png
>> A=[5 7 1;2 -8 -3;6 4 8;1 1 10];
>> A'

ans =

     5     2     6     1
     7    -8     4     1
     1    -3     8    10

Simetrik matris için;

>> A=[1 2 3;2 4 -5;3 -5 6]

A =

     1     2     3
     2     4    -5
     3    -5     6

>> A'

ans =

     1     2     3
     2     4    -5
     3    -5     6

Positive Definite Matrix (Pozitif Tanımlı Matris)

Tanım:

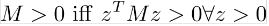
53.png

örnek:

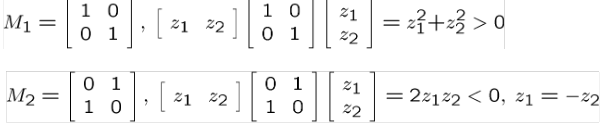
54.png

  • ÖZELLİKLERİ;

    • Tersi alınabilir.

    • Tüm özdeğerleri sıfırdan büyüktür.

    • İzi sıfırdan büyüktür.

    • A, A.AT , AT.A pozitif tanımlıdır.

    • Cholesky decomposition A=LLT

Jacobian Matrix (Jakobiyen Matris)

  • mxn lik karesel olmayan matristir.

  • f(x) bir fonksiyon ve

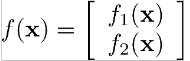
55.png

  • Gradiyent vektörün birinci dereceden kısmi türevini alalım;

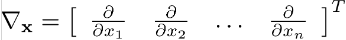
56.png

  • Buradan jakobiyen matris şu şekilde tanımlanır:

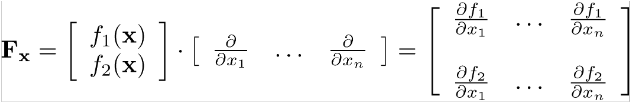
57.png

  • Verilen bir noktada vektör değeri teğet düzleme yönelimlidir.

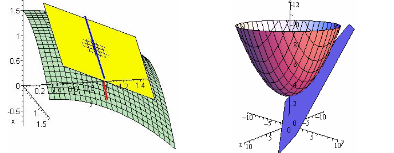
58.png

  • Skaler değerli fonksiyonların gradyentini genelleştirir.

  • Çoğunlukla birinci dereceden hata yayılımında kullanılır.

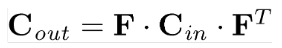
59.png

Quadratic Forms

  • Birçok fonksiyon kuadratik form kullanılarak yerel yakınlaştırılabilir;

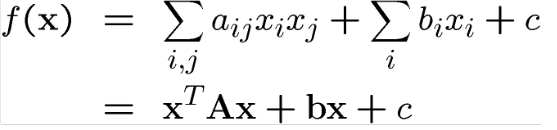
60.png

  • Genellikle tek bir kuadratik formun maksimum yada minimumu bulunur.

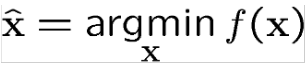
61.png

  • Bu minimizasyon problemine bir çözüm üretmek için matris özelliklerini nasıl kullanabiliriz?

  • f(x)=0

  • Matris çarpımının tanımını kullanarak, f ‘;

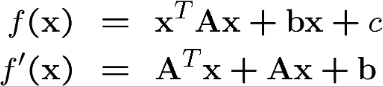
62.png

  • f(x) in minimum değeri türevinin 0 olduğu yerdir;

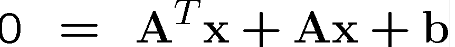
63.png

  • Böylece sistemi çözebiliriz;

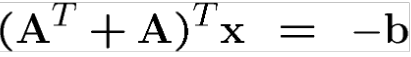
64.png

  • Matris simetrik ise sistem bu hale gelir;

65.png